📚

All Subjects

🤑

AP Micro

⛹🏼‍♀️

Unit 4

4.5 Oligopoly and Game Theory

11 min read•december 23, 2022

dylan_black_2025

Jeanne Stansak

dylan_black_2025

Jeanne Stansak

AP Microeconomics 🤑

95 resources

See Units

What is an Oligopoly?

Brief note before we get started! This section is oftentimes one of the trickiest for students because there aren't really any good graphs or pictures. Instead, we study oligopolies more mathematically using the tools of game theory and good old fashioned intuition. While there is one graph, it's not required for the AP Exam and instead of just a good learning tool. The AP Exam loves giving oligopoly problems, but they only really exist in one form, game theory problems.

An oligopoly is an imperfect market structure where the industry is dominated by a few, large firms. Some good examples of the types of industries that fall in this type of market structure are the cereal industry, oil industry, and automobile industry. Unlike monopolistic competition, there are high barriers and instead of many firms, there are only a couple firms.

Fun Fact! This comes from the Greek oligos for few and the suffix -poly, referring to a market or selling. Hence. oligo-poly, oligopoly! Same reasoning can be applied to a mono- for one, poly: monopoly! Isn't Econ fun? It's fun right? I swear it's fun.

There are two types of oligopolies that can exist:

Colluding oligopolies, otherwise known as cartels - the firms communicate with each other and act as one unit
Non-colluding oligopolies that practice what we refer to as price leadership - the firms compete and do not work together

Characteristics of Oligopolies

Few, large firms - in an oligopoly, there are only a few firms (often less than 10). For example, there are only 3 or 4 major cellular networks: Verizon, T-Mobile, Sprint, and AT&T. There are a few other small ones, but these four companies run roughly the entire market.

Firms are "price makers" - oligopolistic firms experience a degree of market power, so they can control the price somewhat. We'll discuss this more in the context of competition and price leadership as opposed to graphing

High barriers to entry means firms cannot enter the industry - oligopolies are hinged on the fact that they're small markets with few firms. If there were low barriers it is likely the market would turn into something resembling monopolistic competition

Firms earn long-run profits - we won't be calculating profit for an oligopoly, but in general, because of market power, it is likely that an oligopolistic firm earns profits in both the short-run and long-run

Products sold are differentiated with many close substitutes - this is because

Non-price competition is used - this is the big piece of oligopolies. Unlike other markets, the actions of other firms affect the other firms! This is because there are so few firms, so one action by one firm can affect much more of the market. We'll turn to the tools of game theory to figure out how this non-price competition works.

Firms are inefficient if left unregulated - Because price is not equal to marginal cost (necessarily), we are inefficient.

Game Theory

Game theory is the study of how people behave in strategic situations. With the oligopoly market structure, we use a payoff matrix to apply this concept. First, let's look at the fundamentals of game theory and then we'll move into payoff matrices, strategy, and Nash Equilibria.

What is a Game?

In game theory, a game is any set of circumstances that has a result dependent on the actions of two or more decision-makers. In essence, a game is any situation where your actions impact other peoples' actions. This can include what we consider "games" like board games like Battleship, or thought experiments like the prisoner's dilemma.

For our purposes, the players are the firms in the oligopoly. We almost always assume a duopoly, which is an oligopoly with only two firms, since otherwise the math gets really messy. By messy, I mean out of the scope of AP Micro. You'll never need to deal with more than two firms in an oligopoly (that is, until you study economics in college, which you all will. Right?)

Exploring a Payoff Matrix

We represent games in AP Micro using a payoff matrix. A payoff matrix is a chart that shows the actions of two firms and the payoffs (oftentimes represented by the subsequent profit) of each combination of choices.

For example, suppose there are two pizza shops: Tom's Tomatoes and Pete's Pizza. These two firms form a duopoly market for pizza. Now, let's suppose each firm can make one of two choices: Tom can decide whether or not to enter the market, and Pete can decide whether or not he wants to advertise.

The two firms cannot collude, or work together, so while they know what each firm does, they can't control said action. They also work simultaneously, meaning there is no "Pete goes first, Tom goes second". Instead, they each know the payoffs and make a decision at the same time.

Let's break down a theoretical payoff matrix for this situation:

🔽 Pete ///// ➡️ Tom	Enter	Stay Out
Advertise	Pete: $50, Tom: -$2	Pete: $175, Tom: $0
Do Not Advertise	Pete: $150, Tom: $15	Pete: $100, Tom: $0

We see that if Tom stays out, he always makes zero profit (which makes sense, can't make profit if you don't do anything). Alternatively, Tom can make profit if he enters and Pete doesn't advertise. Let's break down what each player should do by looking at two concepts: dominant strategy and Nash Equilibrium.

Dominant Strategies

A dominant strategy is a strategy that a firm should take no matter what the other firm does. Sometimes a firm doesn't have a dominant strategy because they should do different things depending on the other firm. Let's try to determine if either firm has a dominant strategy in our payoff matrix above.

First, let's look at Tom. If Pete advertised, Tom should stay out, since he chooses between losing -$2 or making nothing. If Pete doesn't advertise, Tom should enter, since he can make $15 compared to nothing. Thus, Tom does not have a dominant strategy. This is because there is no "best strategy" regardless of choice.

Now let's look at Pete. If Tom enters, Pete shouldn't advertise ($150 > $50). If Tom stays out, Pete should advertise ($175 > $100). Thus, Pete also doesn't have a dominant strategy.

We'll see in future examples what a dominant strategy looks like, but for this payoff matrix, neither firm has a direct best strategy. There are best options, but they're dependent on the other player. If, for example, Pete made $200 to not advertise if Tom stays out, his dominant strategy would be not to advertise, since no matter what Tom did, Pete was better off not advertising. However, in our case, it depends.

Nash Equilibrium

The Nash Equilibrium of a non-cooperative game like ours is a point at which - and stay with me here - a stable state of a game in which no participant can unilaterally improve their position. The word unilaterally always messes up students, but this definition is actually fairly simple.

All the Nash Equilibrium is is a point at which both players are stable - they cannot improve unless the other player moves, but the other player also can't improve because that would require them to move, so neither move. It's a point at which the game equilibrates (hence Nash Equilibrium) and neither party has an incentive to move without the other player doing so first.

For example, in our case, we have two Nash Equilibria:

1. Do Not Advertise and Enter

2. Advertise and Stay Out

At these two points, neither player stands to gain by changing their decision, assuming the other player doesn't move.

You can find these points by circling the best options for each firm depending on the other player's choice. If there are two circles in any box, we have a Nash Equilibrium, since both players are doing the best they can relative to the other player's choice! We can see this with the highlighting below:

Example Problems

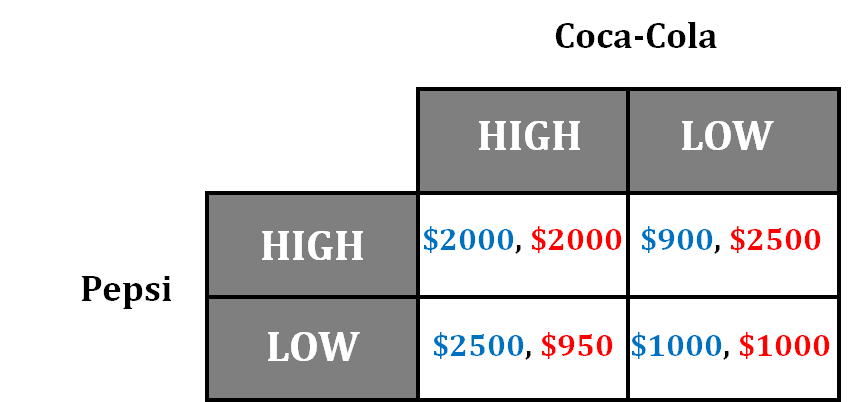
Provided below is a game theory matrix for the soft drink industry. Coca-Cola and Pepsi are oligopolistic firms that collude to dominate the soft drink market. In this scenario, both firms have the choice to set their prices high or low, and the potential profits for both firms are listed in the matrix. The firms are aware of the payoffs but do not collude when making their decision (unless explicitly stated). The numbers on the right of each box (in red) belong to Coca-Cola and the numbers on the left of each box (in blue) belong to Pepsi.

Let's look at some sample questions that are typically asked about these type of problems:

If Coca-Cola and Pepsi collude, what will be the payoff for both firms?
They will both choose to charge a high price and they will both earn a $2,000 profit. (This is the best outcome for both of them while colluding)
Does Coca-Cola have a dominant strategy and if so, what is it?
Yes, the strategy is to charge a lower price. We determine this by finding which pricing strategy will be more favorable for Coca-Cola depending on Pepsi's pricing strategy. If Pepsi goes high, Coca-Cola can either go high and make a $2000 profit, or go low and make a $2500 profit. Since $2500 > $2000, Coca-Cola will go low when Pepsi goes high. If Pepsi goes low, Coca-Cola can either go high and make a $950 profit, or go low and make a $1000 profit. Since $1000 > $900, Coca-Cola will go low when Pepsi goes low. In both situations, Coca-Cola's pricing strategy is the same, which means that going low is their dominant strategy.
Does Pepsi have a dominant strategy and if so, what is it?
Yes, it is to charge a lower price. We determine this by finding which pricing strategy will be more favorable for Pepsi depending on Coca-Cola's pricing strategy. If Coca-Cola goes high, Pepsi can either go high and make a $2000 profit, or go low and make a $2500 profit. Since $2500 > $2000, Pepsi will go low when Coca-Cola goes high. If Coca-Cola goes low, Pepsi can either go high and make a $900 profit, or go low and make a $1000 profit. Since $1000 > $900, Pepsi will go low when Coca-Cola goes low. In both situations, Pepsi's pricing strategy is the same, which means that going low is their dominant strategy.
If Coca-Cola and Pepsi decide NOT to collude and choose their price level on their own, what will be the payoff for both firms? Explain.

Pepsi will have a profit of $1000 and Coca-Cola will have a profit of $1000. Since Coca-Cola has a dominant strategy of a low price and Pepsi has a dominant strategy of a low price, these two decisions meet in the box where Pepsi and Coca-Cola have the profits listed above.

Sample Free Response Question (FRQ): 2007 Question #3

Two bus companies, Roadway and Rankin Wheels, operate a route from Greensboro to Spring City, transporting a mix of passengers and freight. They must file their schedules with the local transportation board each year and cannot alter them during that year. Those schedules are revealed only after both companies have filed. Each company must choose between an early and a late departure. The relevant payoff matrix appears below, with the first entry in each cell indicating Roadway's daily profit and the second entry in each cell indicating Rankin Wheels' daily profit.

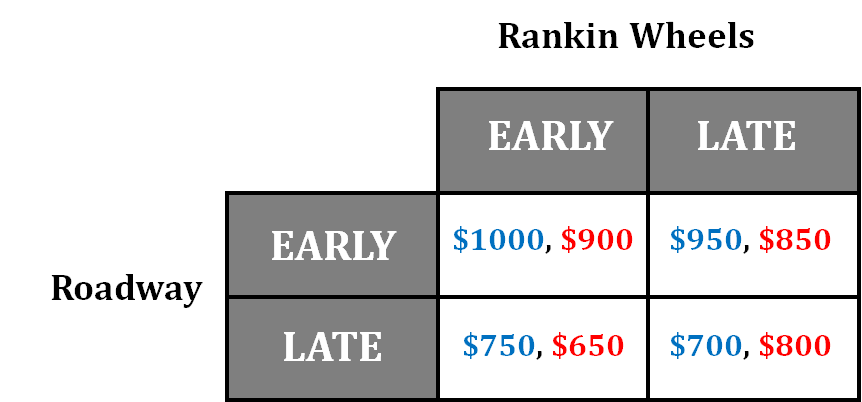
(a) In which market structure do these firms operate? Explain.

The market is an oligopoly because there are only two firms and their actions are mutually interdependent.

(b) If Roadway chooses an early departure, which departure time is better for Rankin Wheels?

Rankin Wheels will choose an early departure because if Roadway is choosing an early departure, then Rankin Wheels' two options are early departure with a profit of $900 or a late departure with a profit of $850. Since $900 is greater than $850, they will choose an early departure.

(c) Identify the dominant strategy for Roadway.

Roadway's dominant strategy is an early departure. When Rankin Wheels departs early, Roadway can make $1000 by departing early or $750 by departing late. When Rankin Wheels departs late, Roadway can make $950 by departing early or $700 by departing late. In both scenarios, early departure results in the highest profit for Roadway ($1000 > $750 and $950 > $700).

(d) Is choosing an early departure a dominant strategy for Rankin Wheels? Explain.

No, because if Roadway chooses a late departure, Rankin Wheels is better off choosing a late departure because $800 profit is greater than $650 from an early departure. However, if Roadway chooses an early departure, Rankin Wheels is better off choosing an early departure because $900 profit is greater than $850 profit from a late departure. Rankin Wheels' does not have a dominant strategy, which means they have to choose based on Roadway's strategy.

(e) If both firms know all of the information in the payoff matrix but do not cooperate, what will be Rankin Wheels' daily profit?

Rankin Wheels' daily profit will be $900.

Kinked Demand Curve for an Oligopoly

In an oligopoly, firms experience price leadership. This is a model of oligopoly where the dominant firm will initiate a price change in the industry. An example of this is when there are three non-colluding gas stations that dominate in a small town. The dominant firm will initiate a price change in the industry.

The other gas stations have two opportunities (1) accept the new price change, or (2) ignore the new price change and keep its price the same. If the other firms choose to accept the new price change, then the market price is changes successfully and they are able to continue to maximize profits. If the other firm chooses to ignore the new price change then it can result in a "price war" where firms are continually changing their price in an attempt to outbid each other.

We can model price competition with a kinked demand curve. Let's break this down.

Let's suppose you and another firm are in a non-colluding duopoly market. You can choose two actions: you can increase your price or decrease your price. The other firm is not colluding with you, so they work against you.

If you increase your price, they're best off ignoring you and not changing their price so consumers go to them. This leads to a more elastic demand for you, since you'll have a dramatic loss in consumers (assuming the other firm makes the right choice). This means with price increases, your consumers are price sensitive.

If you decrease your price, your competitor will match your price and the market will stay relatively similar. This means your demand is relatively inelastic.

When we graph this, we see a kink in the demand curve at what would otherwise be the profit maximizing price and quantity:

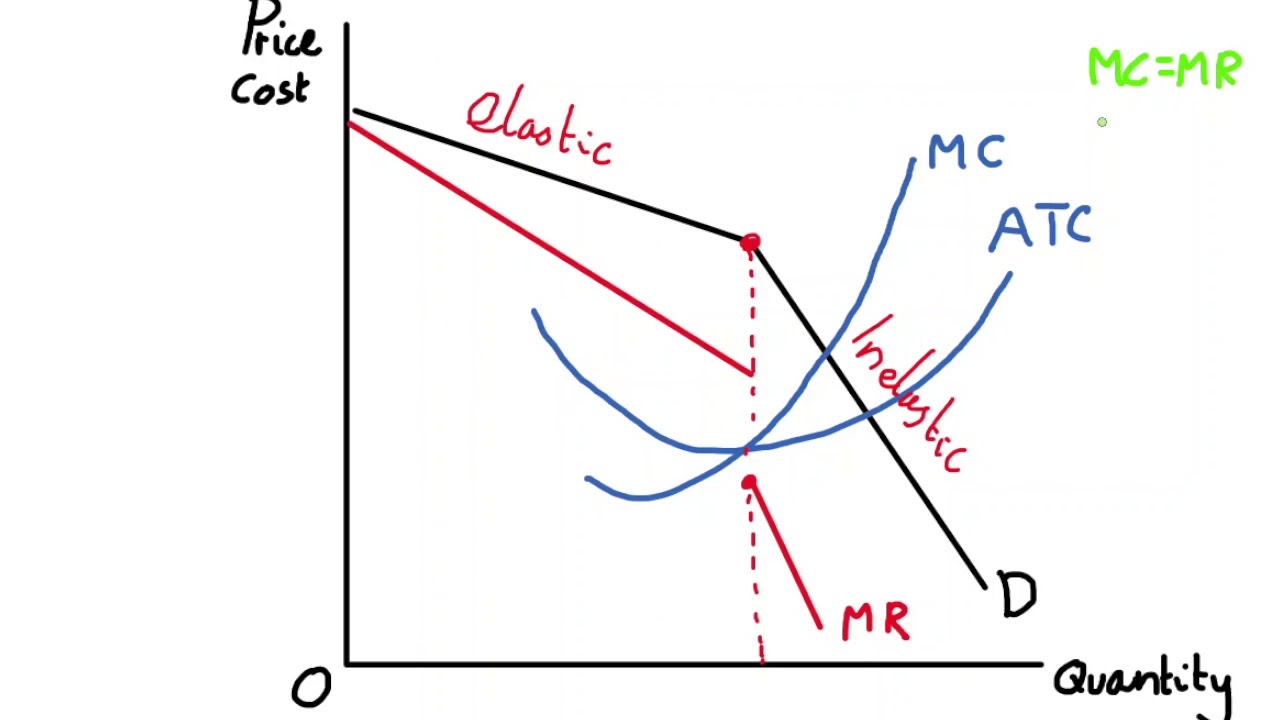
If you're above the equilibrium price (ie. increase), your demand is elastic. Otherwise, it's inelastic. MC and ATC are the same.

This isn't a graph you'll necessarily have to memorize for the AP exam, but helps show how the market is influenced by interdependence.

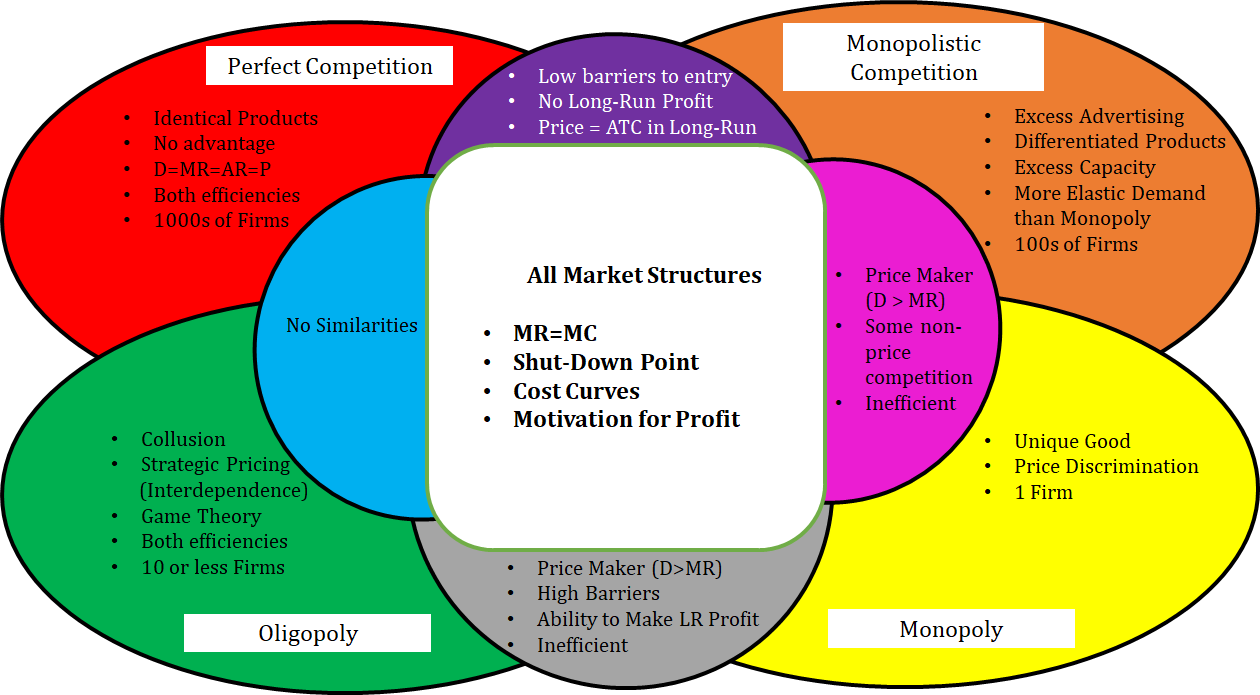
Comparison on All Market Structures

We've officially covered all of the market structures for AP Micro (Except factor markets, but those are somewhat separate)! Here is a chart that compares all four markets that we've discussed so far: