5.3 Rotational Dynamics and Energy
5 min read•january 30, 2023
Daniella Garcia-Loos
Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
Rotational Dynamics Equilibrium and Rigid Body Diagrams
Rotational Dynamics
Rotational Dynamic Equilibrium: This is essentially the rotational analog for Newton's Second Law in which the sum of the net torques is equal to the rotational inertia times the angular acceleration(which should be constant if force is not variable).
ΣTnet=Iɑ
This means that the further away from the axis the greater the torque is! In addition to this force analog, we also have an analog for one of the most important parts of a problem in physics: force diagrams/free body diagrams. This analog is most commonly referred to as a rigid body diagram. It is very similar to an FBD, except you can see where the force is being applied to the diagram! They usually look something like:
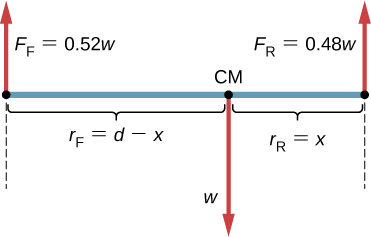
Taken from OpenStax
A large portion of the time you will have to use force diagrams and equations in conjunction with torque!
A rigid body diagram is a visual representation of the forces and moments acting on a rigid object. To draw a rigid body diagram, follow these steps:
- Identify the object and its reference frame. This typically includes the origin and two mutually perpendicular axes.
- Identify the forces acting on the object. These can include forces such as weight, friction, and tension. Draw vectors to represent each force, with the tail of the vector at the point of application and the arrow pointing in the direction of the force.
- Identify the moments acting on the object. Moments are forces that cause rotational motion. They can include torques, moments of inertia, and angular momentum. Draw vectors to represent each moment, with the tail of the vector at the point of application and the arrow pointing in the direction of the moment.
- Sum the forces and moments to find the net force and net moment. Draw a vector to represent the net force, with the tail of the vector at the point of application and the arrow pointing in the direction of the net force. Draw a vector to represent the net moment, with the tail of the vector at the point of application and the arrow pointing in the direction of the net moment.
- Label all vectors with their magnitude and direction, and indicate the reference frame used.
Rolling? Sliding? Rotating? What reaches the bottom first?
If a rigid body is defined as “rolling,” this implies (in the ideal case) that the frictional force does no work on the rolling object. The consequence of this property is that in some special cases (such as a sphere rolling down an inclined surface), the conservation of mechanical energy can be applied to the system.
There is a box, a hoop, and a ball at the top of the frictionless ramp released at the same time, what gets to the bottom first and why?
All three objects, the box, hoop and ball, will reach the bottom of the frictionless ramp at the same time if they are released simultaneously.
This is because they are all subject to the same force, gravity, which acts vertically downward. The ramp is frictionless, so there is no force acting horizontally that would slow any of the objects down. Therefore, the only force acting on the objects is gravity, which would cause them to accelerate vertically downward at the same rate, regardless of their shape or size.
It's important to note that each object will follow a different trajectory based on their individual shapes and characteristics. The box will move vertically down, while the hoop will roll down and the ball will move in a parabolic trajectory. But, all will reach the bottom at the same time as they are subject to the same gravitational force.
What if the ramp has friction?
If the ramp has friction, the box, hoop and ball will not reach the bottom at the same time. The frictional force will act in the opposite direction to the motion of the objects and will slow them down as they move down the ramp.
The amount of friction that each object experiences will depend on the coefficient of friction between the object and the ramp, as well as the normal force acting on the object. The box will experience more friction than the hoop, which will experience more friction than the ball.
The box will experience static friction because the box is not able to roll, so it will have to slide down the ramp. The hoop will experience less static friction and more kinetic friction because it will roll down the ramp. The ball will experience the least amount of friction because it has the smallest contact area with the ramp.
As a result, the box will take longer to reach the bottom of the ramp than the hoop and the ball. The hoop will take longer to reach the bottom than the ball.
Rotational Energy
As with almost everything else that is translational, there is a form of rotational energy! This does not mean that there isn't any other type of energy occurring though! Most of the time there will be a combination of translational and rotational kinetic energy.
Rotational energy, also known as rotational kinetic energy, is the energy that an object possesses due to its rotation around an axis.
Practice Questions:
1)
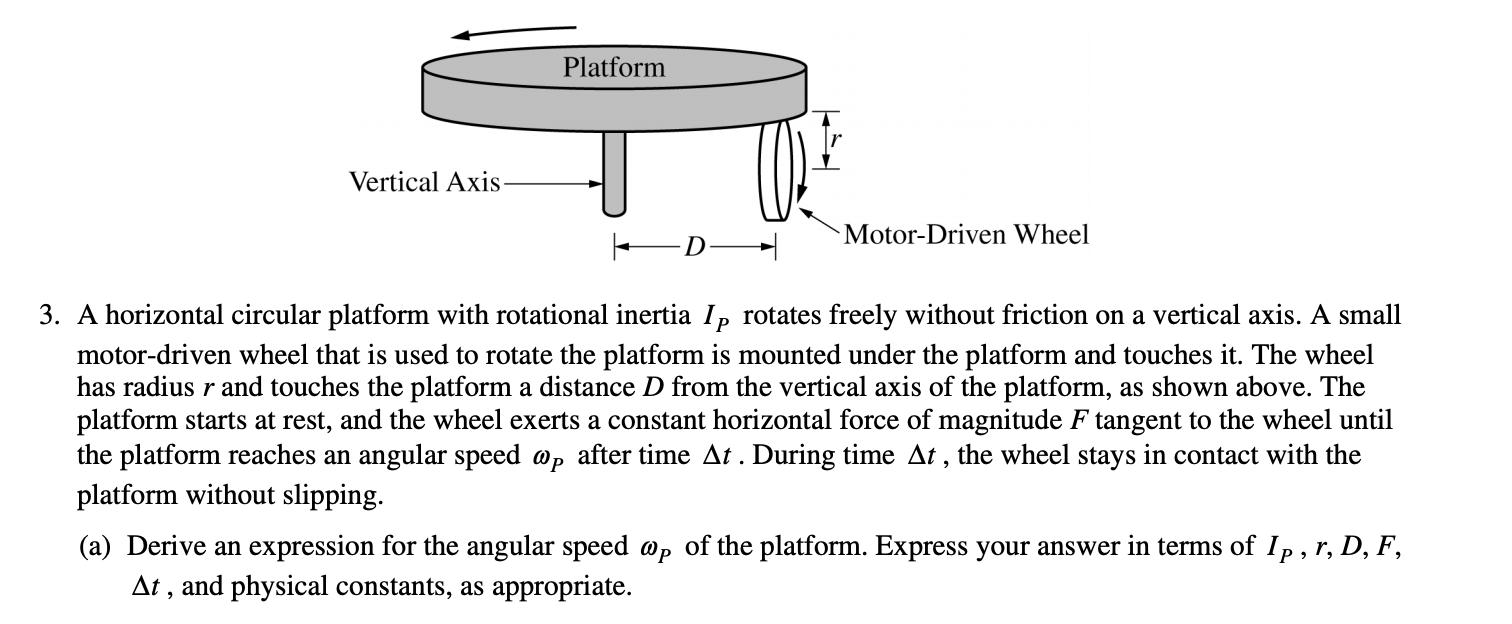
Taken from College Board
Answer:
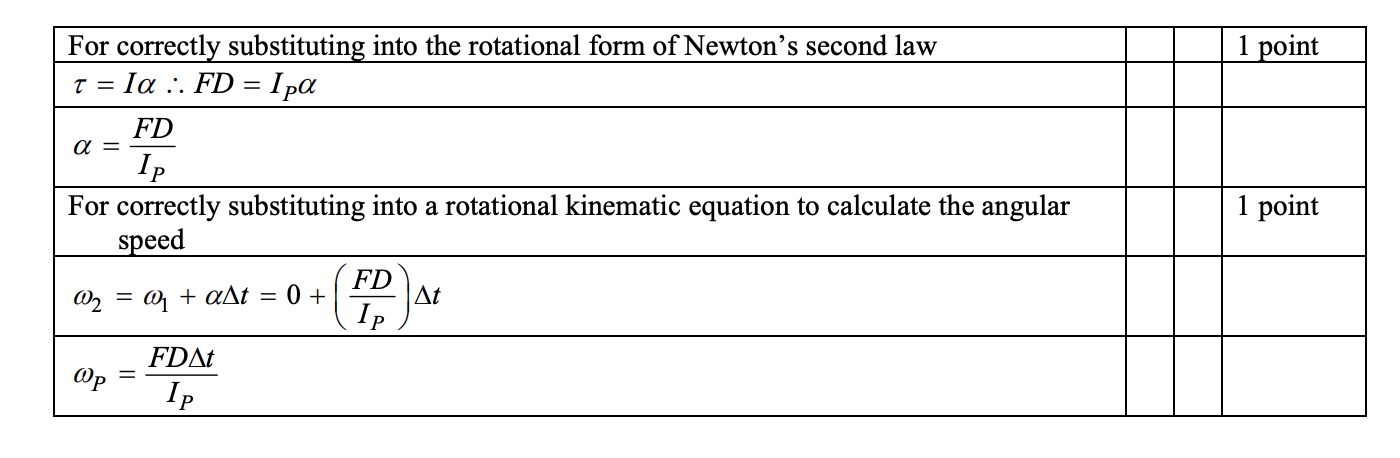
2)

Answer:

3)
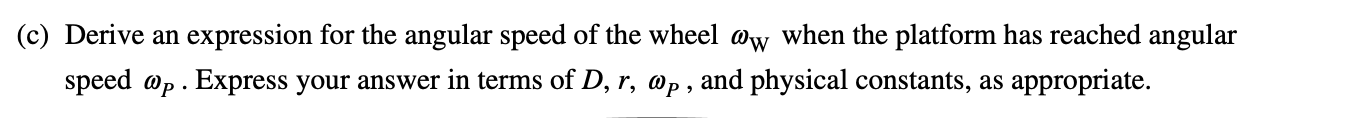
Answer:

4)
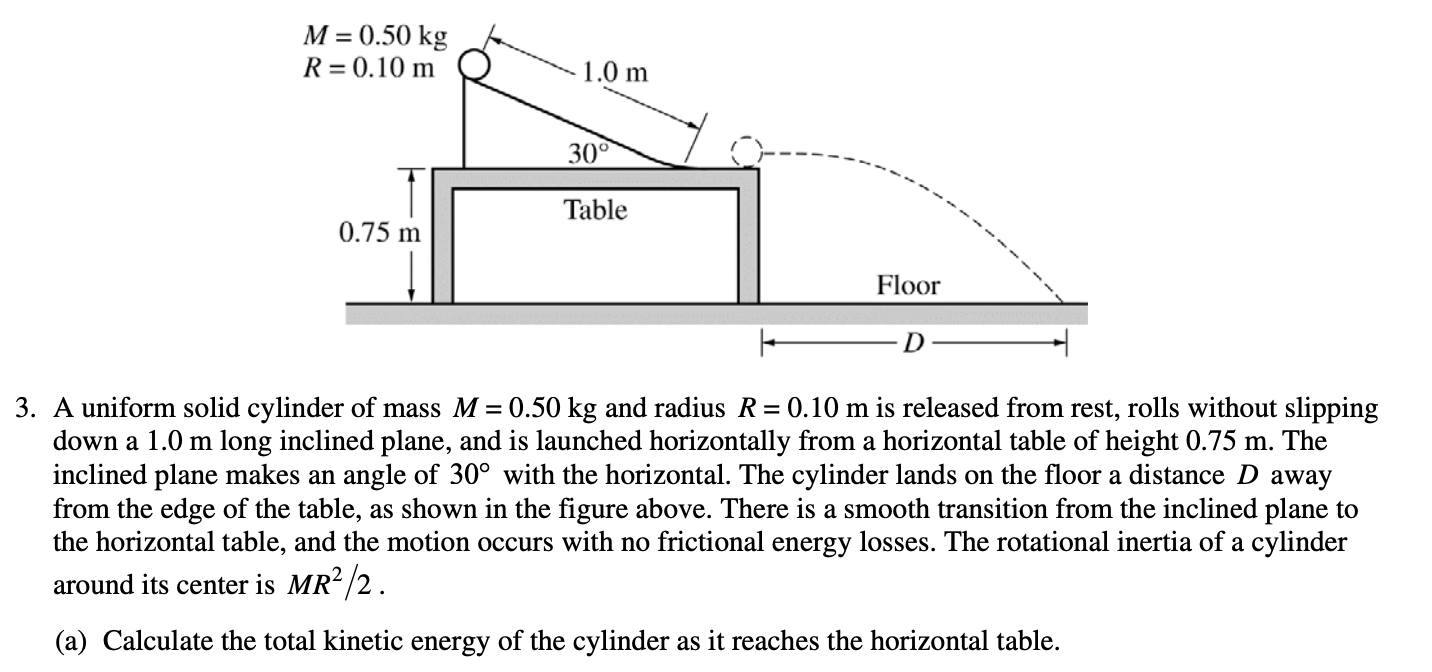
Answer:
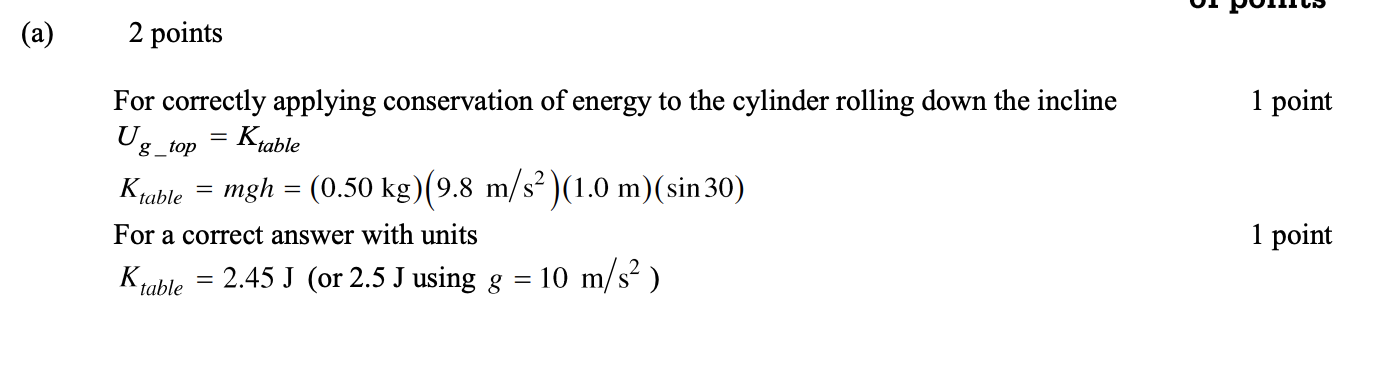
5)

Answer:
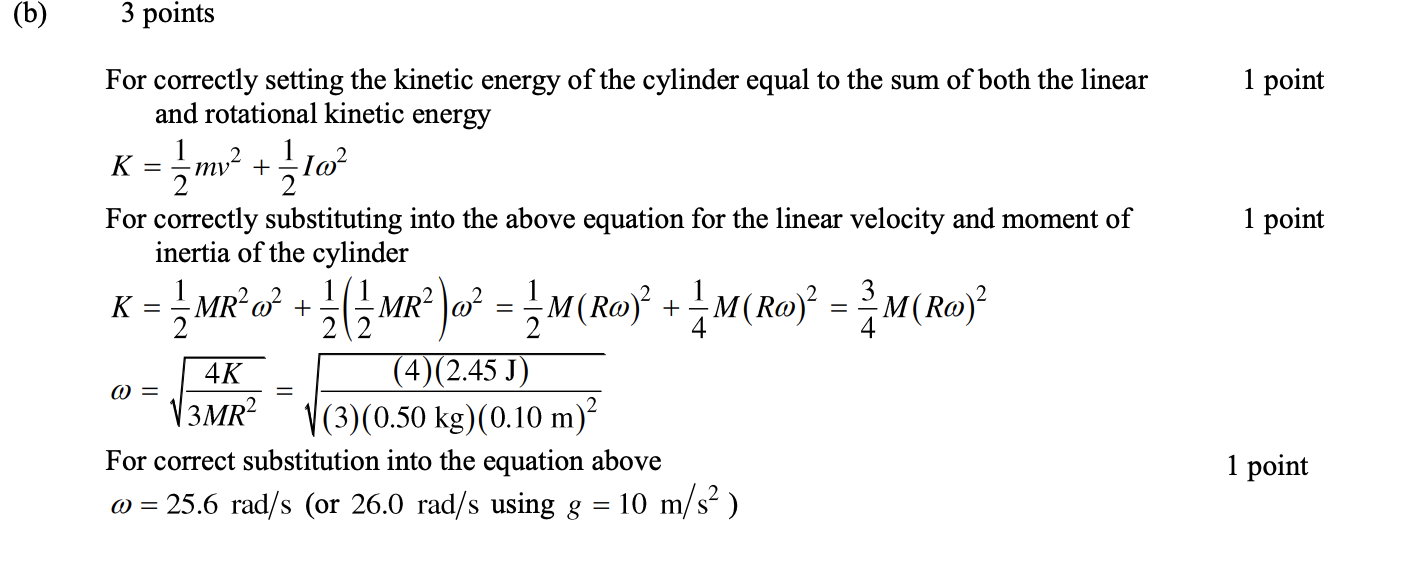
Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
🙏Exam Reviews

© 2023 Fiveable Inc. All rights reserved.